Pascal's Triangle II

Given an index k, return the k^th row of the Pascal's triangle.

For example, given k = 3,
Return [1,3,3,1].

Note:
Could you optimize your algorithm to use only O(k) extra space?

Hint: This is a follow-up question of pascal triangle. An obvious method is to just compute every row of that triangle, and select the k-th row, However, as it is suggested to optimize the algorithm by using only O(k) extra space, we should not do like that.

There is an interesting property of Pascal's Triangle, as shown here

http://en.wikipedia.org/wiki/Pascal%27s_triangle

which indicates that the k-th element of the n-th row in the triangle is given by C_n^k. Then the solution is obvious.

However, a difficulty is how to calculate C_n^k. As factorial operations may result in overflow, we use a safer way to get the value, as

C_n^k=C_{n-1}^{k-1}*n/k
shown from line 20-line 21

Also, as the combination numbers are symmetric, we just calculate half of the values, shown in line 23

01 public ArrayList<Integer> getRow(int rowIndex) {

02     ArrayList<Integer> row=new ArrayList<Integer>();

03     for(int i=0;i<=rowIndex;i++)

04     {

05         int value=(int) combination(rowIndex,i);

06         row.add(value);

07     }

08     return row;

09 }  

10 

11 //calculate C_n^k

12 public long combination(int n, int k)

13 {

14     if(k==0 || k==n)

15         return 1;

16     if(k==1 || k==n - 1)

17         return n;

18     //Just calculate the left half,

19     //as the combination numbers are symmetric    

20     if(k<=(n + 1) / 2)

21         return combination(n - 1,k - 1) * n / k;

22     else

23         return combination(n, n - k);

24   

25 }

However, one may say that the above method uses a recursion function, which will cost the space overhead greater than k. Let's found another property of the combination numbers. We know that

C_n^k=C_{n-1}^k+C_{n-1}^{k-1}

Look familiar, right? 

Remember the Fibonacci number we have met before. To calculate the next number, we add up previous two numbers. Look at the following figure

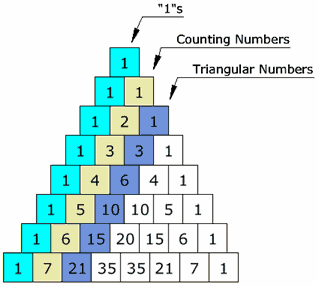
At the 0-th line, we only have one variable 1. 

At the 1-st line, we have two variables x and y both set to 1. 

At the 2-nd line, x is substitute by y, and y is substitute by the 1-th element in the arraylist, which was 1 previously (yellow 1 at the 1-th row). Then we update it as (x+y) and we get 2. Then we simply push "1" as the last element. 

At the 3-rd line, x is substitute by y, which is 1, and y is the 1-st element of the array, which is the yellow 2, we update it to (x+y), which is the yellow three. Then x is substitute by y, which equals 2, and y is the 2-nd element (blue 1), then we get (x+y) and update the 2-nd element, which results the blue 3. In the end we just append 1.

...

01 public ArrayList<Integer> getRow(int rowIndex) {
02     ArrayList<Integer> row=new ArrayList<Integer>();
03     row.add(1);
04     if(rowIndex==0)
05         return row;
06     row.add(1);
07     if(rowIndex==1)
08         return row;
09     for(int i=2;i<=rowIndex;i++)
10     {
11         int x=1;
12         int y=1;
13         for(int j=1;j<i;j++)
14         {
15             x=y;
16             y=row.get(j);
17             row.set(j,x+y);
18         }
19         row.add(1);
20     }
21     return row;
22 }